A few days ago, Ben Orlin of mathwithbaddrawings.com posted Ultimate Tic-Tac-Toe, which described a nested game of Tic-Tac-Toe – In lieu of describing the game again, I’ll direct you to his post if you haven’t already read it.
The problem with UTTT is thus: the Orlin Gambit is too strong, and Ben admits it in his later edit. There, he says that sending a player to an already won board means that they can go anywhere.
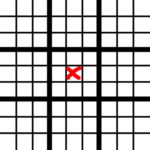
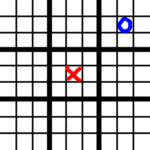
This means that a game start goes like this. X takes the center, which forces O to take a non-center square:
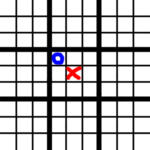
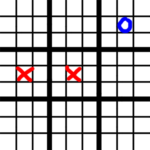
Then X can take the center again, forcing O again to take a non-center square. Since the center square is more desirable than any other, by a longshot, the game almost deterministically ends up in this state:
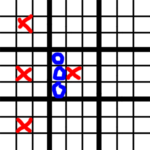
But with the new rules, O can now take any large square they like, but if they take a center small square, then X will be able to choose where to go. Assuming that center squares are the most desirable, the game will end up something like this. (Someone with more time should investigate if there is a better move for O when they get their first free move…)
Notice that it is X’s move, and they already have the center square in 2/3 of the squares! That said, O does have the center square overall, so perhaps this is balanced? It just seems like a lot of moves forced by the game, since the player has otherwise made a “bad” move and worsened their position.
More analysis is needed to see if O taking a not-center-small-square for their fourth turn would turn out well.
So, to fix this, I have a rule change that should alleviate this problem: If a player chooses the center square of a small board, the other player can choose any large board to play in. For example, if X takes the center of the center square on their first move, then O can take the center of any other square.
So now we have a starting game that looks like,
X takes the center of the center:
Since X took a center square, O can choose which large square to play in:
Now X chooses which large square to play in:
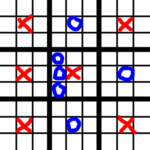
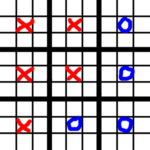
But this means O also gets to choose a square! By now, the game is already up to the players! So we don’t have a forced game past, perhaps, the first move or so. Eventually we will end up with some configuration of (assuming center squares are desirable):
So here, O has at least one more square! And since our assumption that center squares are desirable probably doesn’t hold, either player could force the other to play in a side-large-square at any point up to this.
I hope this “fixes” the game of Ultimate Tic-Tac-Toe and makes it a fun and much deeper game for everyone! I’ll work on getting a javascript version here on the blog eventually. (I’m going to D.C. for the weekend so no promises).
From an Amtrak Train somewhere in New Jersey,
–Erty Seidel
Leave a Reply